>>> import _dictinfo >>> from timeit import timeit >>> def bits(n): ... n += 2**32 ... return bin(n)[-32:] # remove '0b' ... >>> print bits(1) 00000000000000000000000000000001 >>> print bits(-1) 11111111111111111111111111111111 # All timeit() metrics were performed with # Python 2.6 as packaged on Ubuntu 9.10, and # run on my 2GHz Dell Latitude D630. |
The Mighty DictionaryBrandon Craig Rhodes
PyCon 2010 Atlanta
|
|
Q: How can Python lists access
every one of their items
with equal speed?
timeit('mylist[0]', 'mylist = [1] * 9000') # --> 0.053692102432250977 # ~50 ns per getitem timeit('mylist[7000]', 'mylist = [1] * 9000') # --> 0.051460027694702148 # ~50 ns per getitem |
|
A: Python lists use segments of RAM
and RAM acts like a Python list (!)
|
The DictionaryUses keys instead of indexes
and keys can be almost anything
>>> d = { ... 'Brandon': 35, ... 3.1415: 'pi', ... 'flickr.com': '68.142.214.24', ... (2, 6, 4): 'Python version', ... } |
|
How can we turn
the keys dictionaries use
into indexes that reach memory quickly?
|
The Three Rules#1 A dictionary is really a list
|
>>> # An empty dictionary is an 8-element list! >>> d = {} 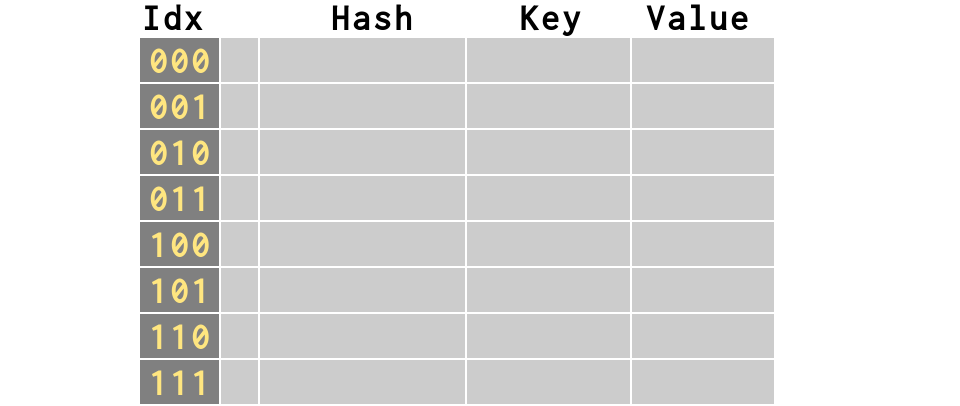
|
>>> # This “list” of “items” is managed >>> # as a “hash table” containing “slots” 
|
The Three Rules
#1 A dictionary is really a list
#2 Keys are hashed to produce indexes
|
|
Python lets you see hashing
in action through the hash() builtin
>>> for key in 'Monty', 3.1415, (2, 6, 4): ... print bits(hash(key)), key 01100111100110010110110011111110 Monty 01101010101011010000100100000010 3.1415 01000111010110111010001100110111 (2, 6, 4) |
|
Quite similar values often have
very different hashes
>>> k1 = bits(hash('Monty')) >>> k2 = bits(hash('Money')) >>> diff = ('^ '[a==b] for a,b in zip(k1, k2)) >>> print k1; print k2; print ''.join(diff) 01100111100110010110110011111110 01100110101101001000101011101001 ^ ^ ^^ ^^^^ ^^ ^ ^^^ |
|
Hashes look crazy, but the same value
always returns the same hash!
>>> for key in 3.1415, 3.1415, 3.1415: ... print bits(hash(key)), key 01101010101011010000100100000010 3.1415 01101010101011010000100100000010 3.1415 01101010101011010000100100000010 3.1415 |
Keys and IndexesTo build an index, Python uses
the bottom n bits of the hash
|
>>> d['ftp'] = 21 >>> b = bits(hash('ftp')) >>> print b 11010010011111111001001010100001 >>> print b[-3:] # last 3 bits = 8 combinations 001 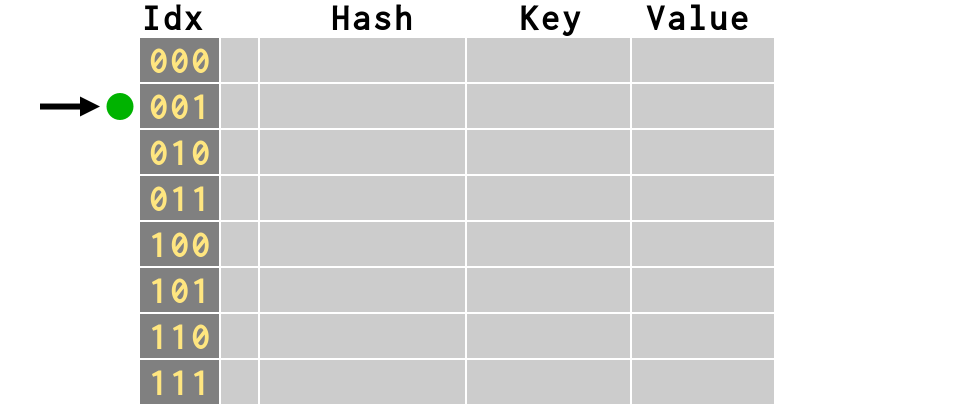
|
>>> d['ftp'] = 21 >>> b = bits(hash('ftp')) >>> print b 11010010011111111001001010100001 >>> print b[-3:] # last 3 bits = 8 combinations 001 
|
>>> d['ssh'] = 22 >>> print bits(hash('ssh'))[-3:] 101 
|
>>> d['ssh'] = 22 >>> print bits(hash('ssh'))[-3:] 101 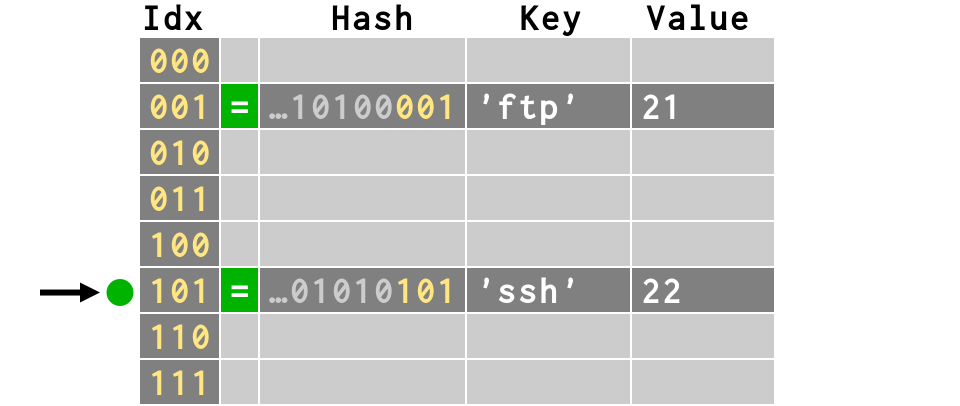
|
>>> d['smtp'] = 25 >>> print bits(hash('smtp'))[-3:] 100 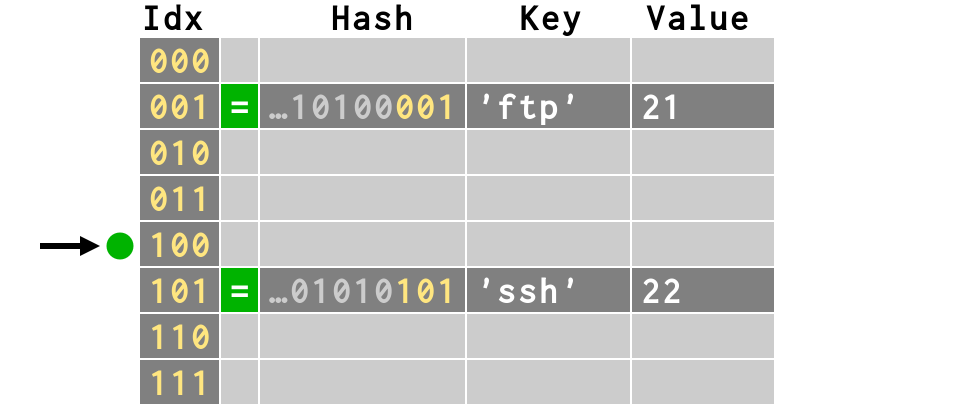
|
>>> d['smtp'] = 25 >>> print bits(hash('smtp'))[-3:] 100 
|
>>> d['time'] = 37 >>> print bits(hash('time'))[-3:] 111 
|
>>> d['time'] = 37 >>> print bits(hash('time'))[-3:] 111 
|
>>> d['www'] = 80 >>> print bits(hash('www'))[-3:] 010 
|
>>> d['www'] = 80 >>> print bits(hash('www'))[-3:] 010 
|
d = {'ftp': 21, 'ssh': 22, 'smtp': 25, 'time': 37, 'www': 80} 
|
Lookup: same 3 steps
|
>>> print d['smtp'] 25 >>> print bits(hash('smtp'))[-3:] 100 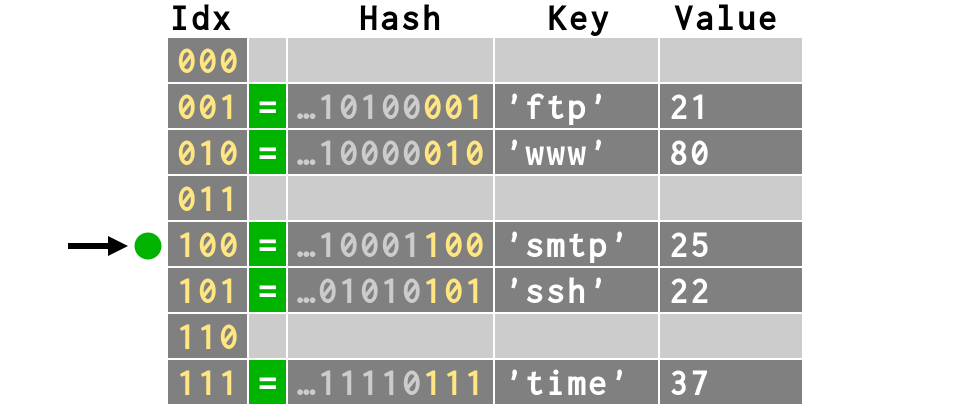
|
Consequence #1Dictionaries tend to return their
contents in a crazy order
|
>>> # Different than our insertion order: >>> print d {'ftp': 21, 'www': 80, 'smtp': 25, 'ssh': 22, 'time': 37} >>> # But same order as in the hash table! 
|
>>> # keys and values also in table order >>> d.keys() ['ftp', 'www', 'smtp', 'ssh', 'time'] >>> d.values() [21, 80, 25, 22, 37] 
|
The Three Rules
#1 A dictionary is really a list
#2 Keys are hashed to produce indexes
#3 If at first you don't
succeed, try, try again
|
“Collision”When two keys in a dictionary
want the same slot
|
>>> # start over with a new dictionary >>> d = {} 
|
>>> # first item inserts fine >>> d['smtp'] = 21 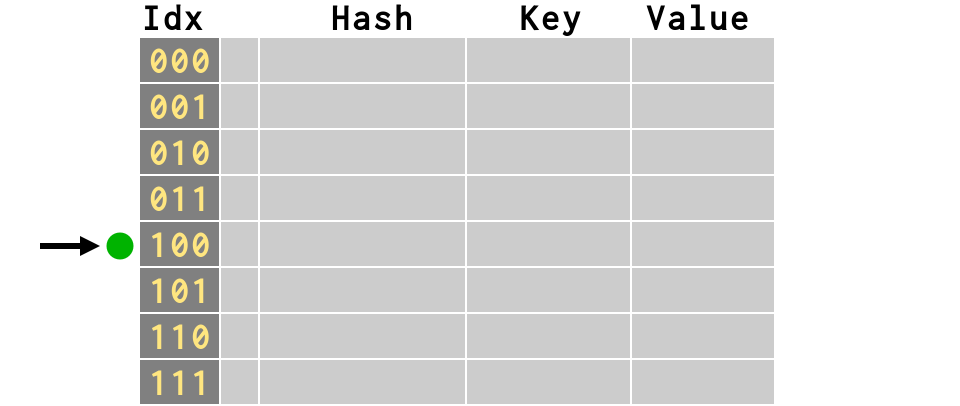
|
>>> # first item inserts fine >>> d['smtp'] = 21 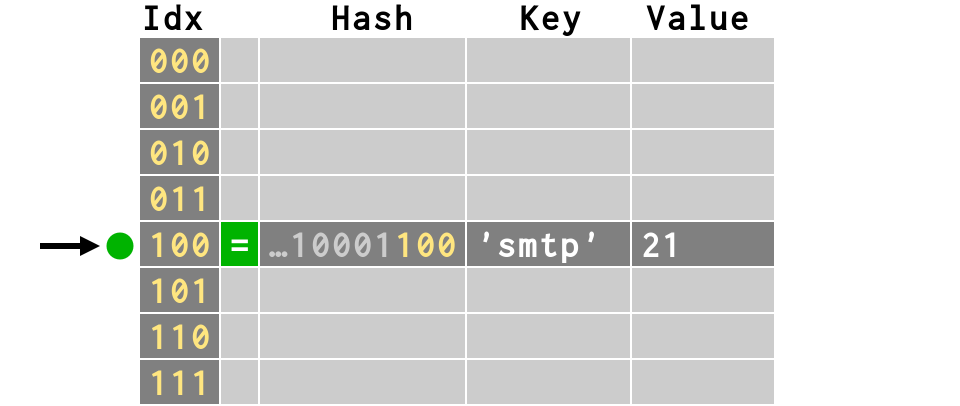
|
>>> # second item collides! >>> d['dict'] = 2628 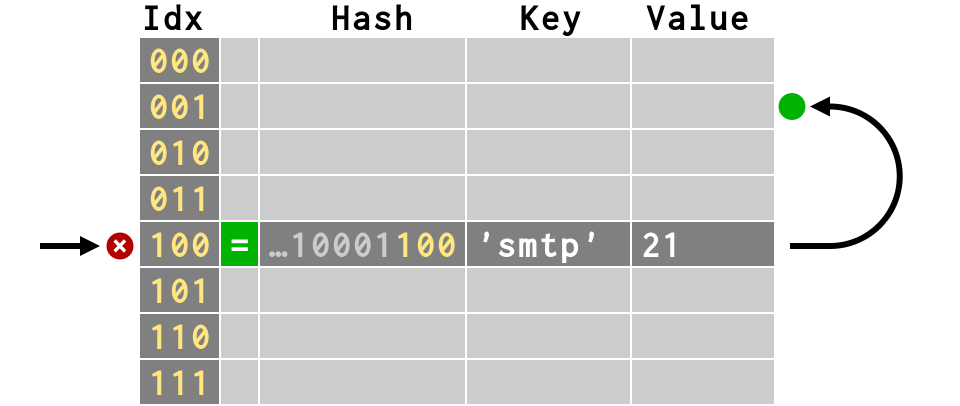
|
>>> # second item collides! >>> d['dict'] = 2628 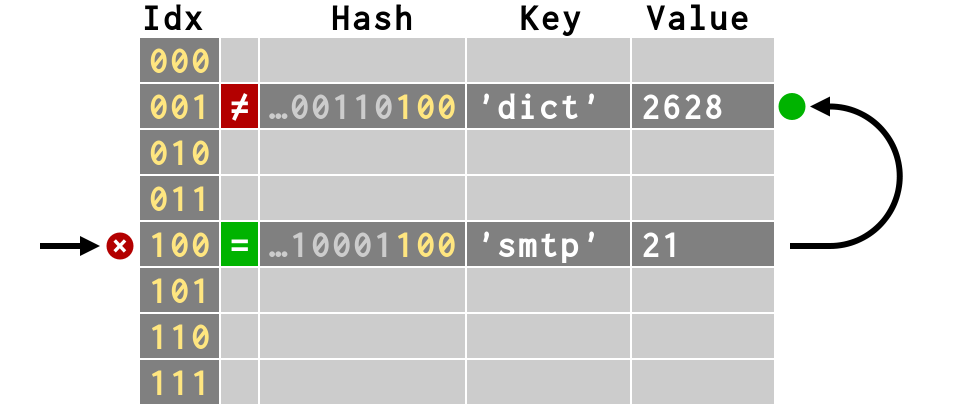
|
>>> # third item also finds empty slot >>> d['svn'] = 3690 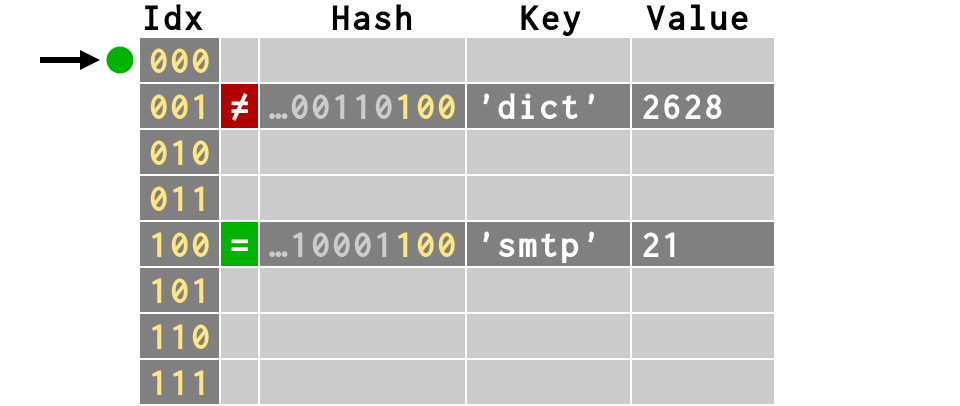
|
>>> # third item also finds empty slot >>> d['svn'] = 3690 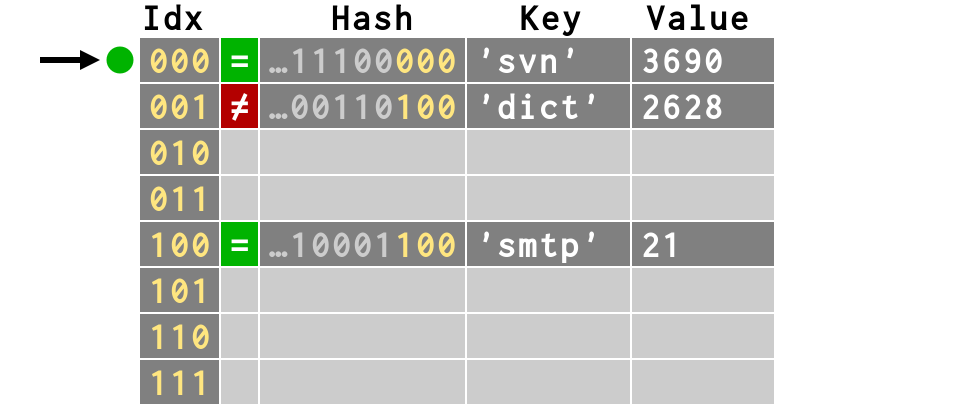
|
>>> # fourth item has multiple collisions >>> d['ircd'] = 6667 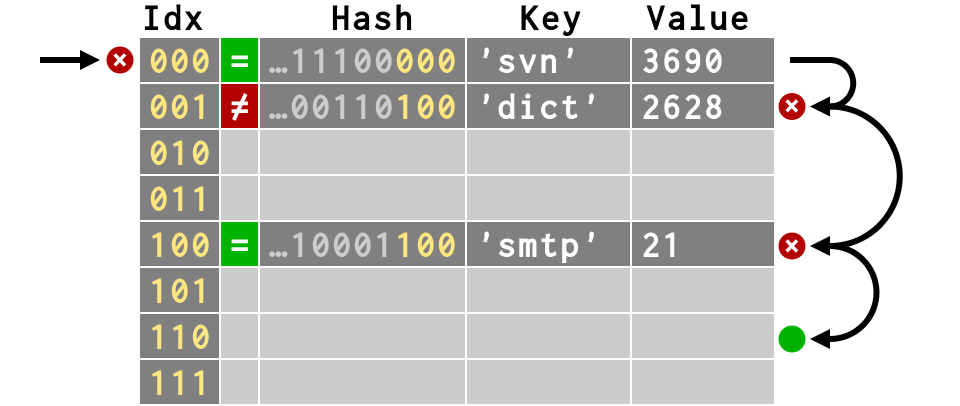
|
>>> # fourth item has multiple collisions >>> d['ircd'] = 6667 
|
>>> # fifth item collides, but less deeply >>> d['zope'] = 9673 
|
>>> # fifth item collides, but less deeply >>> d['zope'] = 9673 
|
# Only ⅖ of the keys in this dictionary # can be found in the right slot 
|
Consequence #2Because collisions move keys
away from their natural hash values,
key order is quite sensitive
to dictionary history
|
>>> d = {'smtp': 21, 'dict': 2628, ... 'svn': 3690, 'ircd': 6667, 'zope': 9673} >>> d.keys() ['svn', 'dict', 'zope', 'smtp', 'ircd'] 
|
>>> e = {'ircd': 6667, 'zope': 9673, ... 'smtp': 21, 'dict': 2628, 'svn': 3690} >>> e.keys() ['ircd', 'zope', 'smtp', 'svn', 'dict'] 
|
The same yet differentAlthough these two dictionaries
are considered equal, their different
histories put their keys
in a different order
>>> d == e True >>> d.keys() ['svn', 'dict', 'zope', 'smtp', 'ircd'] >>> e.keys() ['ircd', 'zope', 'smtp', 'svn', 'dict'] |
Consequence #3The lookup algorithm is actually
more complicated than
“hash, truncate, look”
|
Consequence #3It's more like “until you find
an empty slot, keep looking,
it could be here somewhere!”
|
>>> # Successful lookup, length 1 >>> # Compares HASHES then compares VALUES >>> d['svn'] 3690 
|
>>> # Successful lookup, length 4 >>> d['ircd'] 6667 
|
>>> # Unsuccessful lookup, length 1 >>> d['nsca'] Traceback (most recent call last): ... KeyError: 'nsca' 
|
>>> # Unsuccessful lookup, length 4 >>> d['netstat'] Traceback (most recent call last): ... KeyError: 'netstat' 
|
Consequence #4Not all lookups are created equal.
Some finish at their first slot
Some loop over several slots
|
Stupid Dictionary Trick #1# Because integers hash as themselves, # we can create unlimited collisions! threes = {3: 1, 3+8: 2, 3+16: 3, 3+24: 4, 3+32: 5} 
|
Stupid Dictionary Trick #1# Thanks to piling collisions atop each # other, we can make lookup more expensive timeit('d[3]', 'd=%r' % threes) # -> 0.078 timeit('d[3+32]', 'd=%r' % threes) # -> 0.082 
|
Consequence #5When deleting a key,
you need to leave
“dummy” keys
|
del d['smtp'] # Can we simply make its slot empty? 
|
del d['smtp'] # But what would happen to d['ircd']? 
|
|
When a key is deleted,
its slot cannot simply
be marked as empty
Otherwise, any keys
that collided with it would
now be impossible to find!
So we create a dummy key instead
|
>>> # Creates a <dummy> slot that >>> # can be re-used as storage >>> del d['smtp'] 
|
>>> # That way, we can still find d['ircd'] >>> d['ircd'] 6667 
|
Stupid Dictionary Trick #2>>> del d['svn'], d['dict'], d['zope'] >>> d['ircd'] 6667 >>> # Still requires 4 steps! 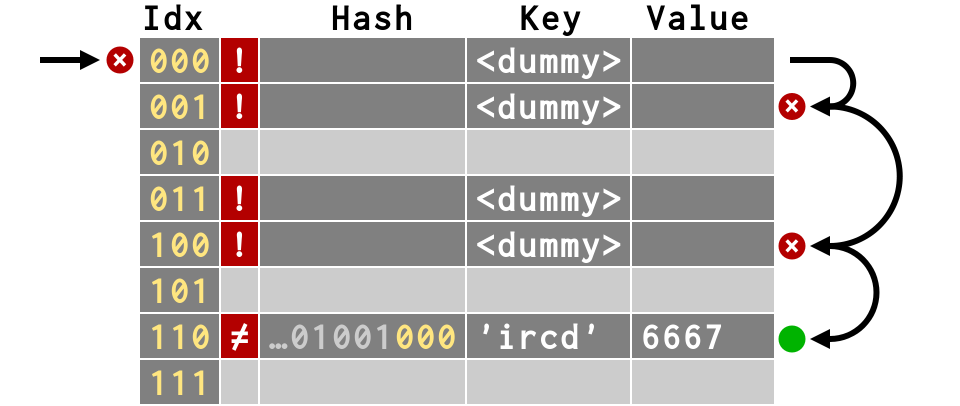
|
Dicts refuse to get fullTo keep collisions rare,
dicts resize when only ⅔ full
When < 50k entries, size ×4
When > 50k entries, size ×2
|
|
Let's watch a dictionary in action
against words pulled from the standard
dictionary on my Ubuntu box
>>> wordfile = open('/usr/share/dict/words') >>> text = wordfile.read().decode('utf-8') >>> words = [ w for w in text.split() ... if w == w.lower() and len(w) < 6 ] >>> words [u'a', u'abaci', u'aback', u'abaft', u'abase', ..., u'zoom', u'zooms', u'zoos', ...] |
d = {} # Again, an empty dict has 8 slots # Let's start filling it with keys 
|
d = dict.fromkeys(words[:5]) # collision rate 40% # but now ⅔ full — on verge of resizing! 
|
d['abash'] = None # Resizes ×4 to 32, collision rate drops to 0% 
|
d = dict.fromkeys(words[:21]) # ⅔ full again — collision rate 29% 
|
d['abode'] = None # Resizes ×4 to 128, collision rate drops to 9% 
|
d = dict.fromkeys(words[:85]) # ⅔ full again — collision rate 33% 
|
|
Life cycle as dictionary fills:
Gradually more crowded as keys are added
Then suddenly less as dict resizes
|
Consequence #6Average dictionary
performance is excellent
|
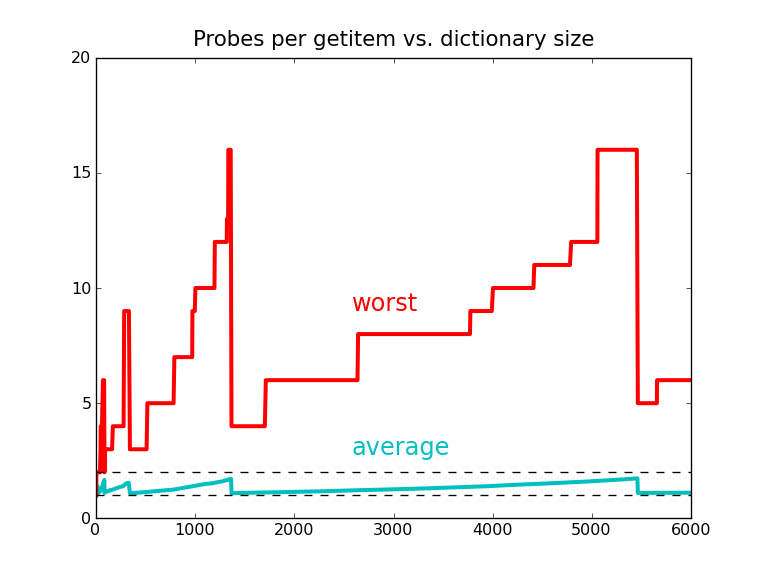
Real-life collisionsA dictionary of common words: >>> wfile = open('/usr/share/dict/words') >>> words = wfile.read().split()[:1365] >>> print words ['A', "A's", ..., "Backus's", 'Bacon', "Bacon's"] We can examine which keys collide: >>> pmap = _dictinfo.probe_all_steps(words) |
|
Some keys are in the first slot probed: >>> pmap['Ajax'] [1330] >>> pmap['Agamemnon'] [2020] While some keys collided several times: >>> pmap['Aristarchus'] # requires 5 probes [864, 1089, 801, 1108, 74] >>> pmap['Baal'] # requires 16 probes! [916, 1401, 250, 1359, 399, 1156, 1722, 420, 53, 266, 1331, 512, 513, 518, 543, 668] |
 |
|
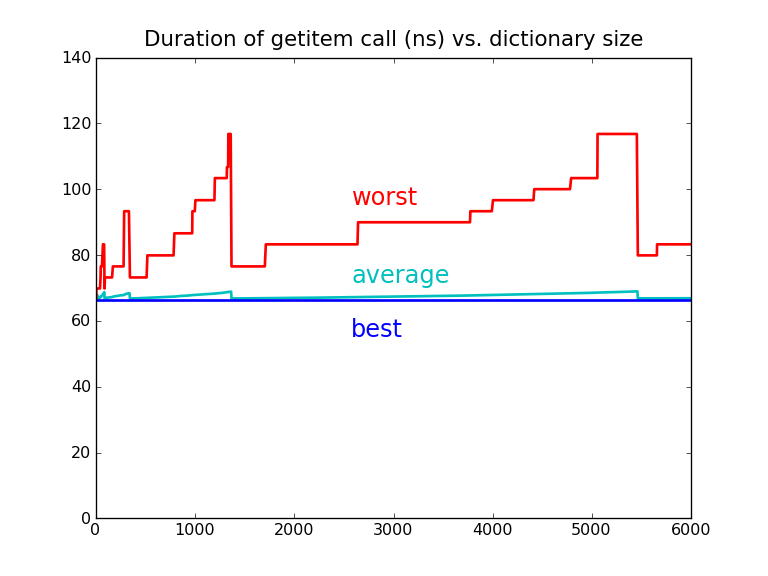
But probes are very fast >>> setup = "d=dict.fromkeys(%r)" % words >>> fast = timeit("d['Ajax']", setup) >>> slow = timeit("d['Baal']", setup) >>> '%.1f' % (slow/fast) '1.7' |
 |
Consequence #7Because of resizing,
a dictionary can completely reorder
during an otherwise innocent insert
>>> d = {'Double': 1, 'double': 2, 'toil': 3, ... 'and': 4, 'trouble': 5} >>> d.keys() ['toil', 'Double', 'and', 'trouble', 'double'] >>> d['fire'] = 6 >>> d.keys() ['and', 'fire', 'Double', 'double', 'toil', 'trouble'] |
Consequence #8Because an insert can radically
reorder a dictionary, key insertion
is prohibited during iteration
>>> d = {'Double': 1, 'double': 2, 'toil': 3, ... 'and': 4, 'trouble': 5} >>> for key in d: ... d['fire'] = 6 Traceback (most recent call last): ... RuntimeError: dictionary changed size during iteration |
Take-away #1Hopefully “the rules”
now make a bit more sense
and seem less arbitrary
|
Take-away #2Dictionaries trade space for time
If you need more space,
there are alternatives
|
Take-away #3If your class needs its own __hash__()
method you now know how hashes
should behave
(You can often get away with ^ xor'ing
the hashes of your instance variables)
|
Hashing your own classesclass Point(object): def __init__(self, x, y): self.x, self.y = x, y def __eq__(self, p): return self.x == p.x and self.y == p.y def __hash__(self): return hash(self.x) ^ hash(self.y) |
Take-away #4Equal values
should have equal hashes
regardless of their type!
>>> hash(9) 9 >>> hash(9.0) 9 >>> hash(complex(9, 0)) 9 |
The End May your hashes be unique,
Your hash tables never full,
And may your keys rarely collide
|
Other materialHow much time does malloc take? Both on going bigger and smaller!
|